Starting to think about performance

We’ve talked about making programs more readable and concise, but we haven’t yet thought much about making programs fast (or efficient in other ways).

Here’s a Python program:

def count_the(l: list) -> int:
    count = 0
    for s in l:
        if s == 'the':
            count += 1
    return count

What’s the running time of the count_the function? One way to find out would be to actually time an execution on some real data. We could load in Frankenstein again, call the function on the list that split() returns, and actually time it.

tim@somerville sep24 % python3 lecture08.py frankenstein.txt
That file had 4066 appearances of the word "the".

That went by far faster than we could actually count with a stopwatch. We could tell our terminal to time execution for us:

tim@somerville sep24 % time python3 lecture08.py frankenstein.txt
That file had 4066 appearances of the word "the".
/usr/local/bin/python3  frankenstein.txt  0.06s user 0.04s system 28% cpu 0.347 total

This is a lot of information, but for now just notice the 0.347 total, which says the program took around a third of a second in total.

This approach has some flaws. What are they?

Think, then click!

  • Some of the time will be taken up by starting the program, loading the file into memory, and other operations that have nothing to do with the runtime of the single function count_the.

  • Our stopwatch only tells us the runtime for a specific computer, under a specific existing workload, in a specific environment. There will also be some randomness involved.

  • This tells us how long the program takes on Frankenstein, but what about other inputs? How is the function likely to scale as the books get bigger? We can’t run the function on all possible books, so how can we really predict its performance overall?


Runtime vs. Scaling

The truth is that, when we talk about how time-efficient a program is, there are two very different things we might mean:

Which question you’re asking depends on what problems you’re trying to solve. For today, we’ll focus on the second question: how well does a program scale?

Let’s see if we can figure out a rough estimate of how long it takes to run count_the without actually running it. We can start by counting the “basic operations,” like adding numbers or assigning to a variable, executed in the function:

def count_the(l: list) -> int:
    count = 0           # 1 creation, 1 assignment
    for s in l:         # repeat: len(l) times
        if s == 'the':  #     1 (short) string comparison
            count += 1  #     1 add, 1 assignment
    return count       # 1 to return

So for an arbitrary list of length L, the program might execute up to $3L+3$ operations:

This might sound way too imprecise. Not all operations take the same amount of time (and there’s a fair bit of variation across different computers). We are losing some precision, but we’re gaining generality. Here’s what I mean:

If we’re really concerned with how our function’s performance scales as inputs get bigger, the exact details of how long an operation takes often become irrelevant. Because of that, we’ll say that the running time of count_the is _proportional to (3 * L) + 3.

Notice that we’re making many assumptions, or at least abstracting out quite a few details. We’re not counting the for-loop itself as an operation; do we need to? Python’s operations probably don’t actually take the same amount of time; does it matter?

For some purposes, the answers to these questions absolutely matter. Some code is run inside Google’s servers every time a user does a web search. The exact running time of that code is very important to Google! But even in professional engineering, when you’re picking an algorithm or data structure (more on this later) the exact runtime is nearly always less important than how your choice will scale.

In fact, even this much precision is more than we’ll generally use. It’s hard to be sure about how long specific operations take: if returning from a function takes a while, then the real runtime could be more like (3 * L) + 100. If addition takes a while it could be (50 * L) + 3. So we’ll focus on the most important value here: the input list length. We’ll say that our function’s running time is linear in L, because everything else washes out at scale. The program does some constant amount of work for each element of the list, plus some additional constant amount of work.

Two more examples

Next class we’ll introduce some commonly-used notation for expressing this idea. But before that, let’s look at a couple more functions.

Example 1: testing membership in a list

How about this one?

def is_member_of(l: list, ele) -> bool:
    for x in l:
        if x == ele:
            return True
    return False

How long does this function take, for a list of length L?

The running time of member depends on its arguments even more than the running time of count_the did!

Best Case: If we call it on a list whose first element is ele, it really doesn’t matter how long the list is. It’s going to check the first element and no more, so it’ll take the same, constant, amount of time regardless of how long the list is. We can express this by saying that the best case time is constant.

Computer programming is an engineering discipline, though. If I’m building a bridge, I’m probably not all that interested in the maximum weight it can tolerate under ideal conditions! What we’re usually interested in (though we’ll see some exceptions, later in the course) is worst-case behavior. For us, that’s: how long will the function take on the worst possible input or inputs?

Worst Case: If ele isn’t actually in l, then the loop in is_member_of needs to traverse the entire list. As with count_the, we’ll say that in its worst-case, the function takes linear time in the length of l.

Example 2: removing duplicates from a list

Take a look at one last function:

def distinct(l: list) -> list:
    seen = []
    for x in l:
        if x not in seen:
            seen.append(x)
    return seen

This one is a bit more complicated. The for loop runs once for every element in the list, but how long does every iteration of the loop take? To figure that out, we need to learn something about how lists function in Python.

In Python, x not in seen is basically equivalent in to calling our previous example function is_member_of. To check membership in a list, Python will walk the list just like our function did. But that means every time the for loop in distinct runs, that single iteration takes linear time in the length of seen.

Best Case: What’s the best case? Well, if all of the elements in l are the same, x not in seen never takes more than a constant number of operations. So in that case, the function runs in linear time.

Worst Case: How about the worst case? What if the elements are all different?

Think, then click!

If all the elements are different, then every x will be new, and thus won’t be found in the seen list. But then the size of the seen list grows every time the loop iterates: at first it’s 0, then 1, then 2, and so on.

Some geometric intuition might be useful here:

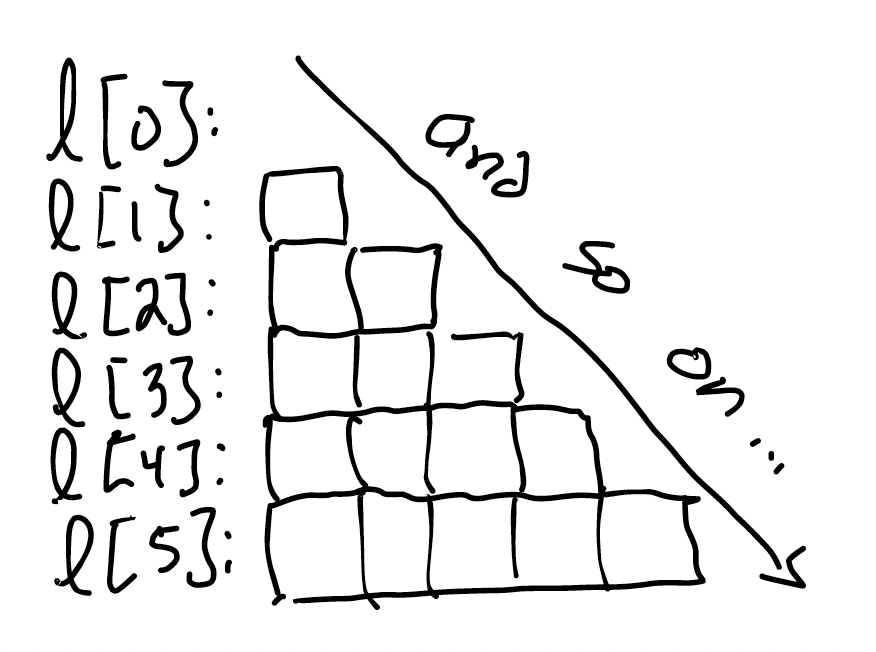
How many blocks are there in this diagram? $(0 + 1 + 2 + … + (L - 1))$ of them. With a little algebra, this simplifies to $\frac{L (L + 1)}{2}$. This is a quadratic equation; if we were to multiply it out, there’d be a $L^2$ in it. In the worst case, this function will scale with the square of the length of the input. We’ll call this quadratic time.


How much worse is this? Does it actually matter in practice? Let’s find out. We’ll time how long it takes to run count_the on the text of Frankenstein, and how long it takes to run distinct on the same input.

tim@somerville sep24 % time python3 lecture08.py frankenstein.txt
That file had 4066 appearances of the word "the".
/usr/local/bin/python3  frankenstein.txt  0.06s user 0.04s system 28% cpu 0.347 total

tim@somerville sep24 % time python3 lecture08.py frankenstein.txt
That file had 12179 unique words (including caps, punctuation, etc).
python3  frankenstein.txt  2.18s user 0.04s system 84% cpu 2.648 total

The difference is actually quite noticeable even without a timer. Fractions of a second to full seconds. An order of magnitude.

What if we tried on a larger book? I’ve downloaded the full text of an English translation of Mallory’s The Death of Arthur, which is a bit longer:

tim@somerville sep24 % wc frankenstein.txt
    7743   78122  448821 frankenstein.txt
tim@somerville sep24 % wc arthur.txt
   34131  368286 1965003 arthur.txt

(That’s 78122 words versus 368286 words.)

tim@somerville sep24 % time python3 lecture08.py arthur.txt
That file had 14681 appearances of the word "the".
/usr/local/bin/python3  arthur.txt  0.10s user 0.04s system 42% cpu 0.336 total

tim@somerville sep24 % time python3 lecture08.py arthur.txt      
That file had 15790 unique words (including caps, punctuation, etc).
/usr/local/bin/python3  arthur.txt  8.35s user 0.09s system 94% cpu 8.901 total

Now it’s an even bigger gap! Nearly 9 seconds (increased from under 3) to get the unique words in arthur.txt, but hardly any change (around a third of a second) to count how many times "the" appears. And it’ll only get worse as the data gets bigger—unless we get lucky and the input happens to be closer to the best case.

Looking ahead: Sets

But where else do these differences appear? Let’s run a quick experiment between minor changes to the distinct function.

def distinct_list(l: list) -> list:
    seen = []
    for x in l:
        if x not in seen:
            seen.append(x)
    return seen

def distinct_set(l: list) -> list:
    seen = set()
    for x in l:
        if x not in seen:
            seen.add(x)
    return list(seen) # convert back to a list

Try running each of these on Frankenstein. On my laptop, with sets: 0.054 total and with lists: 2.153 total. Both numbers are in seconds.

It seems like there’s a huge impact on performance. In fact, the version that uses sets performs around the same as count_the did last time, and count_the had worst-cast runtime linear in the input size. That is, its worst-case performance was in $O(n)$. It seems like using a set has somehow eliminated the linear cost from the x not in seen check.

I wonder…

Is there a potential bug lurking in the switch from distinct_list to distinct_set? Hint: it depends on what you might need to use the output for.

Why does runtime matter?

It’s useful to consider the ways that runtime matters in the world. People often point out that a faster program uses less electricity and therefore has a lower climate impact. While this is true, I personally tend to be skeptical of generalizing this, since faster execution also makes room for running more programs.

Sure, there are lots of business-focused reasons to have fast code, but there is at least one social factor: access. When building software, we don’t know what kind of computer our eventual users will have. A laptop that a highly-paid developer in San Diego or New York might consider “average” could be a powerful and expensive luxury for others. Even if our program is running in the cloud, performance (realized as cost) could make the difference between someone being able to do analysis and giving it up.

That said, performance isn’t as important as we might initially think. The general advice is: get it right first, and then get it fast. There are exceptions to every rule, but this one is almost always worth following. Especially in 0112.