Implementing Dictionaries

These notes are being released in draft form; they may be modified up until the date of class.

Making a Reasonable Tradeoff: Hash Functions

Can we find a happy medium between these solutions? Maybe by spending a little bit of extra space, we can somehow end up with constant-time lookup? And even if we don’t always manage that, maybe we can still improve on both the extremes above.

Let’s start with another design question. Suppose we want to map the IDs of CSCI 0112 staff to their corresponding name. Further, let’s say that IDs are non-negative numbers ranging between 0 and 999999, but that there are far fewer than a million staff members: there are fewer than 10, and so you’ll never have more than 10 datapoints to store in a given semester.

So I’m going to give you a Python list with just 10 elements to work with. Strictly speaking, that ought to be enough space, but nowhere near enough to make a list cell for every possible ID. Here’s what it looks like:

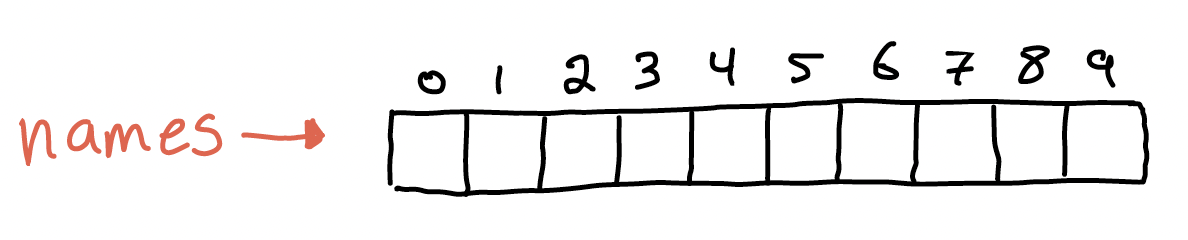
How can we convert a 6-digit student ID to a unique index between 0 and 9?

We can’t.

But what if we were willing to give up the “unique” part of that question? Do we know a way to convert an ID to a number between 0 and 9 (while still making a reasonable effort at uniqueness?)

Every ID has a remainder when divided by 10. For instance, 1234 has remainder 4 when divided by 10. Let’s try using this as our index function. We’ll insert two datapoints: {1234 : 'Tim'} and {5678: 'Ashley'}.

Now if we want to look up the key 5678 we can do so in constant time! Just divide by 10 to get 8, and do a lookup in this Python list.

This sounds great, but do we yet have a usable data structure? What’s the problem?

A Note on Terminology

This kind of key-to-index transformation is often called a hash function, where “hash” here means a digest or summary of the original data. Hash functions are usually fast, lossy, and (in applications beyond this lecture!) built to have a relatively uniform distribution of hashes over the key population to reduce the chance of collision.

The Challenge: Collisions

You’ll learn more about the details if you take CSCI 0200. In short, there are a few ways of handling collisions: my favorite is storing a separate list for every index. Then, if two elements get hashed to the same location, Python can store them both in the sub-list. Searching now needs to loop through the entire sub-list, and with a good hash function elements are usually (but not necessarily) uniformly distributed between locations in the top-level list. It might look something like this:

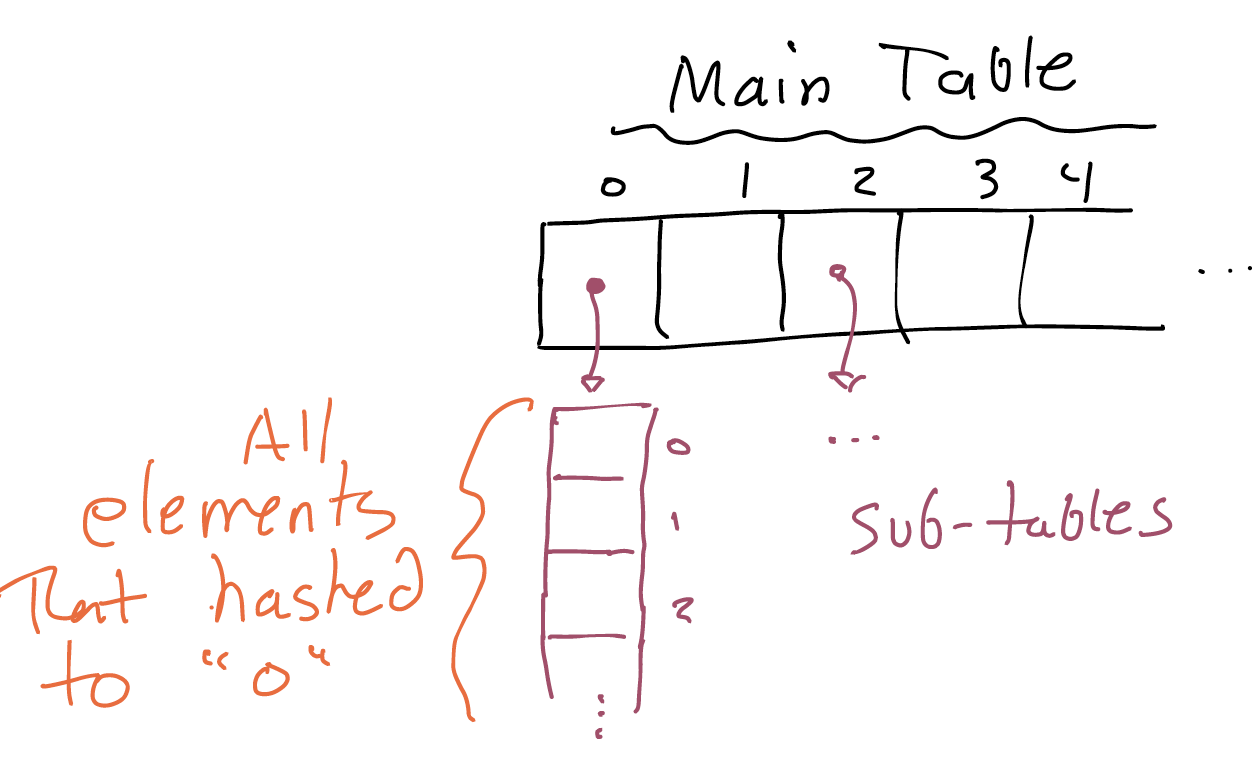
The important takeaway is that, in the worst case (all keys hash to the same index, nothing but collisions) searching a hash table is as slow as a list: linear in the number of elements being stored. With a well-chosen hash function, and enough space in the table, collisions turn out to be rare. With some probability theory, we could prove that the average case is constant time. It’s usually incredibly fast, and anyway never scales worse than a list.

That’s how sets and dictionaries are so fast in Python, and that’s why data structure choice matters!

Making A Simple Hash Table

Let’s do another code-arrangement exercise. This time we’ll be writing a real hash-table, using the sublist method of collision-handling. You’ll fill in 3 functions:

def add(table: list, element: str):
    '''Add an element to the hash-table set'''
    
def search(table: list, element: str):
     '''search for an element in the hash-table set'''

def demo(table_size: int, num_elements: int, element_length: int):
    '''Add a large number of random elements to the hash-table set, then
        show how well-distributed the random elements were'''

Using these lines:

table[idx].append(element)
table = [[] for _ in range(table_size)]
print([len(sublist) for sublist in table])
idx = hash(element) % len(table)
if element not in table[idx]:
idx = hash(element) % len(table)
return element not in table[idx]
idx = hash(element)
if element in table[idx]:
random_element = ''.join(choices(ascii_letters + digits, k=element_length))
for _ in range(num_elements):
return element in table[idx]
add(table, random_element)

Note that, unlike last time, you might not need all of these. I’ve also used list-comprehension and a random-choice library you won’t have seen before. What’s the point? To show you that you don’t need to know exactly how to do a low-level thing in Python to be able to know how to start solving the problem.

You can find a solution in the livecode.

Testing Our Hash Table

We’ve got 2 functions to test (the demo function is just a demonstration).

• Our add function modifies the state of objects in memory. Specifically, it modifies the table list, and potentially all sublists contained in it.
• Our search function doesn’t modify the state, but it does depend on that state.

Remember that, when we’re testing side effects (e.g., adding elements to our table) we can’t just write assertions by themselves. We need to assert something about the effects on the state. E.g., for add maybe we could create an empty table and then see if it contains what we expect.

But how should we check what the table contains? Since the hash of every element, changes between program runs, we can’t rely on the location of an element being consistent. And just checking to see if any sublist contains the element is too broad, since search will only check a single sublist. Let’s just use search. E.g.,

def test_single_element():
    table = [[] for _ in range(10)]
    add(table, 'Hi, everybody!')
    assert search(table, 'Hi, everybody!') == True    
    # ...once this function returns, `table` disappears
    # future tests can make their own `table` list

What other tests would you write?

Note on Dataclasses

Recall that Python’s analogue to Pyret’s data definitions is called a dataclass. (See this 0111 textbook chapter.) E.g.:

 @dataclass
 class Location:
      lat: int
      long: int

If you want to use a dataclass as a key, you need to tell Python that the data cannot be changed by using the frozen=True annotation, like this:

 @dataclass(frozen=True)
 class Location:
      lat: int
      long: int

There is a lot more to hash tables than we have time to discuss in 0112. If you want to learn more (without official 0112 support) about how hashing works in Python, check out the documentation on the __hash__ method of objects. If you want to learn more in the context of a course, check out 0200.